Note
This static document was automatically created from the output of a jupyter notebook.
Execute and modify the notebook online here.
Implementing Beamformers#
This Jupyter notebook will outline the step-by-step process of implementing a new receiving beamformer within the HermesPy framework, using the Minimum Variance Distortionless Response (MVDR, also known as [Cap69]) beamformer as a working example.
As an initial step we will import all required modules:
[2]:
import numpy as np
from hermespy.beamforming import ReceiveBeamformer
The Capon beamformer estimates the power \(\hat{P}\) received from a direction \((\theta, \phi)\), where \(\theta\) is the zenith and \(\phi\) is the azimuth angle of interest in spherical coordinates, respectively. Let \(Y \in \mathbb{C}^{M \times N}\) be the the matrix of \(N\) time-discrete samples acquired by an antenna arrary featuring \(M\) antennas and
\begin{equation} \mathbf{R} = \mathbf{Y}\mathbf{Y}^{\mathsf{H}} \end{equation}
be the respective sample correlation matrix. The antenna array’s response towards a source within its far field emitting a signal of small relative bandwidth is \(\mathbf{a}(\theta, \phi) \in \mathbb{C}^{M}\). Then, the Capon’s spatial power response is defined as
\begin{equation} \hat{P}_{\mathrm{Capon}}(\theta, \phi) = \frac{1}{\mathbf{a}^{\mathsf{H}}(\theta, \phi) \mathbf{R}^{-1} \mathbf{a}(\theta, \phi)} \end{equation}
with
\begin{equation} \mathbf{w}(\theta, \phi) = \frac{\mathbf{R}^{-1} \mathbf{a}(\theta, \phi)}{\mathbf{a}^{\mathsf{H}}(\theta, \phi) \mathbf{R}^{-1} \mathbf{a}(\theta, \phi)} \in \mathbb{C}^{M} \end{equation}
being the beamforming weights to steer the sensor array’s receive characteristics towards direction \((\theta, \phi)\), so that
\begin{equation} \tilde{\mathbf{y}}(\theta, \phi) = \mathbf{w}^\mathsf{H}(\theta, \phi) \mathbf{Y} \end{equation}
are the estimated signal samples impinging onto the sensor array from said direction.
The structure of receiving beamformers is implemented as an abstract prototype in the ReceiveBeamformer. Prototypes specify several abstract properties and methods which inheriting classes must implement. For receiving beamformers those are
num_receive_input_streams - Number of antenna streams the beamformer can process.Our Capon implementation will always require the samples of all device antennas.
num_receive_output_streams - Number of antenna streams the beamformer generates after processing.Since the Capon beamformer focuses the power towards a single direction of interest per estimation, a single stream of samples will be generated after beamforming.
num_receive_focus_angles - Number of angles of interest the beamformer requires for its configuration.The same logic as before applies, only a single direction of interest per beamforming operation is required.
_decode() - This subroutine performs the actual beamforming, given an array of baseband samples, assumed carrier frequency and the angles of interest. This is where the Capon algorithm is being implemented.
[3]:
class CaponBeamformer(ReceiveBeamformer):
def __init__(self, *args, **kwargs) -> None:
ReceiveBeamformer.__init__(self, *args, **kwargs)
@property
def num_receive_input_streams(self) -> int:
return self.operator.device.antennas.num_receive_antennas
@property
def num_receive_output_streams(self) -> int:
return 1
@property
def num_receive_focus_angles(self) -> int:
return 1
def _decode(self,
samples: np.ndarray,
carrier_frequency: float,
angles: np.ndarray) -> np.ndarray:
# Compute the inverse sample covariance matrix R
sample_covariance = np.linalg.inv(samples @ samples.T.conj() + np.eye(samples.shape[0]))
# Query the sensor array response vectors for the angles of interest and create a dictionary from it
dictionary = np.empty((self.num_receive_input_streams, angles.shape[0]), dtype=complex)
for d, focus in enumerate(angles):
array_response = self.operator.device.antennas.spherical_phase_response(carrier_frequency, focus[0, 0], focus[0, 1])
dictionary[:, d] = sample_covariance @ array_response / (array_response.T.conj() @ sample_covariance @ array_response)
beamformed_samples = dictionary.T.conj() @ samples
return beamformed_samples[:, np.newaxis, :]
And that’s it, by specifying three properties and the decode routine a new beamformer has been implemented within HermesPy. We can now plot the beamforming characteristics towards a signal impinging from \((\theta = 0, \phi = 0)\) by calling PlotReceivePattern() and compare it to the CoventionalBeamformer:
[4]:
from hermespy.beamforming import ConventionalBeamformer
_ = CaponBeamformer.PlotReceivePattern()
_ = ConventionalBeamformer.PlotReceivePattern()
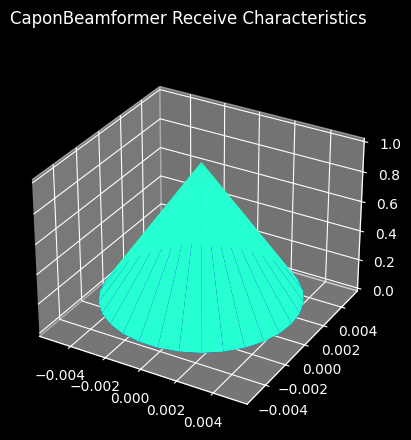
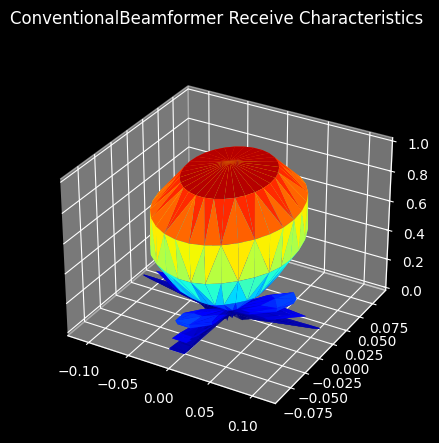
We may now use the newly created beamforming class to configure receive signal processing chains within HermesPy. For example, within an imaging radar application simulation:
[ ]:
import numpy as np
from scipy.constants import pi, speed_of_light
from hermespy.core import dB, ConsoleMode, UniformArray, IdealAntenna
from hermespy.channel import SingleTargetRadarChannel
from hermespy.simulation import Simulation
from hermespy.radar import Radar, FMCW, ReceiverOperatingCharacteristic
# Create a new simulation featuring a single device transmitting at 10GHz
simulation = Simulation(console_mode=ConsoleMode.SILENT)
device = simulation.scenario.new_device(antennas=UniformArray(IdealAntenna(), .5 * speed_of_light / 10e9, (3, 3)))
device.carrier_frequency = 10e9
radar_channel = SingleTargetRadarChannel(target_range=10., radar_cross_section=1., attenuate=False)
simulation.scenario.set_channel(device, device, radar_channel)
# Configure a radar operation on the device
radar = Radar()
radar.device = device
radar.waveform = FMCW()
radar.receive_beamformer = ConventionalBeamformer()
simulation.add_evaluator(ReceiverOperatingCharacteristic(radar, radar_channel))
simulation.new_dimension('snr', dB(-18, -21, -25))
simulation.num_samples = 1000
radar.receive_beamformer.probe_focus_points = np.array([[0., 0.]])
result = simulation.run()
_ = result.plot()
radar.receive_beamformer.probe_focus_points = np.array([[.5*pi, .5*pi]])
result = simulation.run()
_ = result.plot()
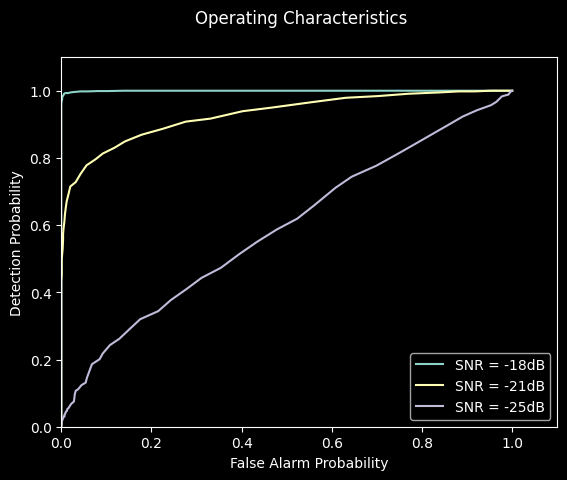
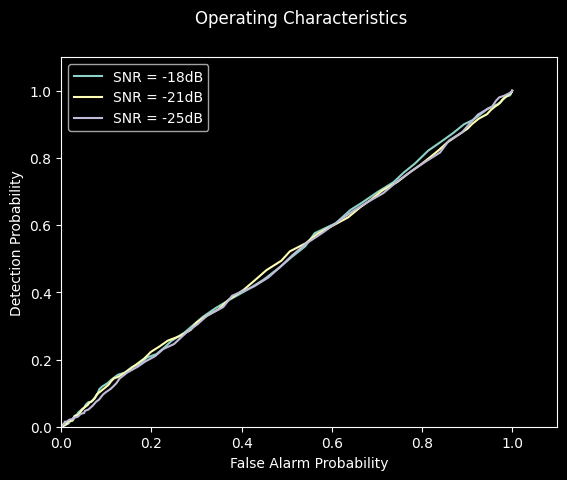
2023-07-12 12:17:15,153 ERROR import_thread.py:80 -- ImportThread: <_MultiThreadedRendezvous of RPC that terminated with:
status = StatusCode.UNKNOWN
details = "Stream removed"
debug_error_string = "UNKNOWN:Error received from peer ipv4:127.0.0.1:65423 {grpc_message:"Stream removed", grpc_status:2, created_time:"2023-07-12T10:17:15.152759853+00:00"}"
>
Exception in thread ray_listen_error_messages:
Traceback (most recent call last):
File "C:\Users\Stealth\AppData\Local\Programs\Python\Python310\lib\threading.py", line 1016, in _bootstrap_inner
2023-07-12 12:17:15,155 ERROR worker.py:914 -- print_logs: <_MultiThreadedRendezvous of RPC that terminated with:
status = StatusCode.UNKNOWN
details = "Stream removed"
debug_error_string = "UNKNOWN:Error received from peer ipv4:127.0.0.1:65423 {grpc_message:"Stream removed", grpc_status:2, created_time:"2023-07-12T10:17:15.153007658+00:00"}"
>
self.run()
File "C:\Users\Stealth\AppData\Local\Programs\Python\Python310\lib\threading.py", line 953, in run
self._target(*self._args, **self._kwargs)
File "d:\envs\hermes-310\lib\site-packages\ray\_private\worker.py", line 2004, in listen_error_messages
_, error_data = worker.gcs_error_subscriber.poll()
File "d:\envs\hermes-310\lib\site-packages\ray\_private\gcs_pubsub.py", line 300, in poll
self._poll_locked(timeout=timeout)
File "d:\envs\hermes-310\lib\site-packages\ray\_private\gcs_pubsub.py", line 217, in _poll_locked
fut.result(timeout=1)
File "d:\envs\hermes-310\lib\site-packages\grpc\_channel.py", line 744, in result
raise self
grpc._channel._MultiThreadedRendezvous: <_MultiThreadedRendezvous of RPC that terminated with:
status = StatusCode.UNKNOWN
details = "Stream removed"
debug_error_string = "UNKNOWN:Error received from peer ipv4:127.0.0.1:65423 {grpc_message:"Stream removed", grpc_status:2, created_time:"2023-07-12T10:17:15.152992559+00:00"}"
>