Note

This static document was automatically created from the output of a jupyter notebook.

Execute and modify the notebook online here.

Implementing FEC codings

This Jupyter notebook will outline the step-by-step process of implementing a new coding scheme for the forward error correction in communication modems. The selected algorithm is a repetition encoder, since it is arguably the most basic error correction coding.

As an initial step, we will import all required modules from HermesPy:

import numpy as np
from hermespy.fec import Encoder

Error correcting coding steps are represented by the abstract Encoder interface. Each coding algorithm is represented by a class inheriting from the interface, which requires them to implement the abstract functions and properties

• encode

• decode

• bit_block_size

• code_block_size

Let’s assume our repetition coding takes blocks of \(K = 4\) data bits and repeats them \(3\) times. The resulting code block size would be \(N = 3K = 12\), which results in a rate of \begin{equation} \mathbf{R} = \frac{K}{N} = \frac{1}{3} \end{equation} for the full encoding. During decoding, the repetition coding decides by majority voting which bit has been transmitted. So, our coding implementation is

class RepetitionCoding(Encoder):

    @property
    def bit_block_size(self) -> int:
        return 4

    @property
    def code_block_size(self) -> int:
        return 12

    def encode(self, data: np.ndarray) -> np.ndarray:
        return np.tile(data, 3)

    def decode(self, code: np.ndarray) -> np.ndarray:
        return (np.mean(np.reshape(code, (3, self.bit_block_size)), axis=0, keepdims=False) > .5).astype(int)

Now we can inspect our coding implementation:

coding = RepetitionCoding()
print(f"Our coding rate is {coding.rate} with an input block size of {coding.bit_block_size} and an output block size of {coding.code_block_size}")

data = np.random.randint(0, 2, coding.bit_block_size)
print(f"Let's assume we transmit the following data block: {data}")

code = coding.encode(data)
print(f"After encoding the respective code block is: {code}")

error_code = code.copy()
error_code[0] = not error_code[0]
print(f"After channel propagation the first bit has flipped: {error_code}")

corrected_data = coding.decode(error_code)
print(f"But the coding can correct a single bit flip to: {corrected_data}")

Our coding rate is 0.3333333333333333 with an input block size of 4 and an output block size of 12
Let's assume we transmit the following data block: [0 1 1 1]
After encoding the respective code block is: [0 1 1 1 0 1 1 1 0 1 1 1]
After channel propagation the first bit has flipped: [1 1 1 1 0 1 1 1 0 1 1 1]
But the coding can correct a single bit flip to: [0 1 1 1]

We may now investigate our newly created forward error correction coding within a full Hermes simulation capaign.

from hermespy.core import ConsoleMode, dB
from hermespy.simulation import Simulation
from hermespy.modem import BitErrorEvaluator, DuplexModem, RootRaisedCosineWaveform

# Create a new simulation featuring a single device transmitting at 10GHz
simulation = Simulation(console_mode=ConsoleMode.SILENT)
device = simulation.scenario.new_device(carrier_frequency=10e9)

# Configure a communication operation on the device, using our coding
modem = DuplexModem()
modem.waveform = RootRaisedCosineWaveform(modulation_order=4, oversampling_factor=2, num_preamble_symbols=0, num_data_symbols=10, symbol_rate=1e6)
modem.encoder_manager.add_encoder(coding)
device.add_dsp(modem)

# Run a very low-demanding simulation for demonstration purposes
simulation.new_dimension('noise_level', dB(0, 4, 8, 16, 18, 20), device)
simulation.add_evaluator(BitErrorEvaluator(modem, modem))
simulation.num_samples = 1000

result = simulation.run()

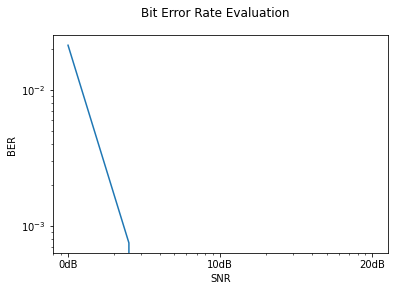
This allows us to visualize the achieved bit error rates for given linear signal to noise ratios:

_ = result.plot()